The following project proposal is for fourth-year students taking the mathematical sciences final-year undergraduate project module for the academic year 2025/2026.
What drives the incredible diversity of life on Earth, and how can mathematics help us understand how it evolved? This project invites you to use your problem-solving skills to uncover the mathematical principles behind evolutionary change. You’ll learn how small variations in traits can lead to big shifts in populations over time—and how these changes can be predicted, analyzed, and understood using mathematical tools. This project offers an opportunity to apply your mathematical skills to real-world questions such as understanding the origins of cooperation, the emergence of new species, or the long-term dynamics of ecosystems.
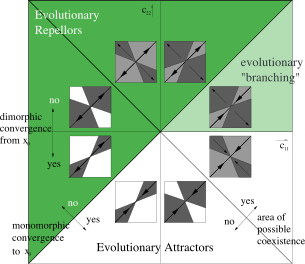
The heart of the project lies in mastering adaptive dynamics, a mathematical framework for modelling how traits evolve through mutation and natural selection in continuous trait spaces. You might investigate questions such as: under what conditions does a population split into distinct evolutionary branches (evolutionary branching)? How do cooperation and competition shape evolutionary stable strategies? Will a disease evolve to become more or less virulent? This project offers the chance to develop and analyze models of evolutionary processes using differential equations, phase portraits, and stability and bifurcation analysis. You will also use computational tools to solve and analyse differential equations.
Prerequisites
Students should be familiar with basic concepts in differential equations and dynamical systems. Prior coding experience and an interest in mathematical modeling in the applied sciences would be helpful. This project best suits students who have taken Mathematical Biology III or Dynamical Systems III.
Resources
Strogatz, S. H. (2001). Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering. [introductory text on nonlinear dynamics].
Diekmann, O. (2004). A beginner’s guide to adaptive dynamics. Banach Center Publications, 63, 47-86.
Nowak, M. A. (2006). Evolutionary Dynamics: Exploring the Equations of Life.