The following project proposal is for third-year students taking the mathematical sciences final-year undergraduate project module for the academic year 2025/2026.
This project explores the theoretical foundations and practical applications of numerical bifurcation analysis, an essential technique for understanding how the qualitative behaviour of dynamical systems evolves as system parameters change. The initial phase of the project will involve a thorough review of the mathematical theory underlying bifurcations, focusing on concepts such as fixed points, stability, and the classification of bifurcation types, including saddle-node, pitchfork, and Hopf bifurcations. Building on this theoretical groundwork, the project will then shift to studying numerical techniques for detecting and following bifurcation points in systems of ordinary differential equations (ODEs) and simple partial differential equations (PDEs). Key numerical methods will be introduced, including continuation algorithms such as pseudo-arclength continuation and deflation techniques. Students will be expected to both study and implement these methods computationally. Time permitting, the project may also introduce more advanced topics, such as the computation and visualization of stable and unstable manifolds, or global bifurcations like homoclinic and heteroclinic connections.
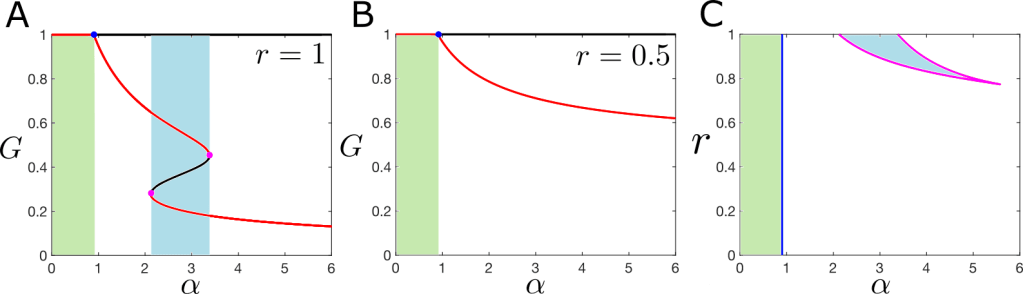
The project’s second phase will focus on applying numerical bifurcation tools to real-world dynamical models drawn from biology, chemistry, physics, or ecology. The aim is to provide hands-on experience exploring how parameter variation affects system dynamics, using case studies such as predator-prey models, chemical oscillators, or reaction-diffusion systems. Students will gain familiarity with established numerical continuation software packages, such as AUTO, MATCONT, or BifurcationKit. They will use these tools to generate bifurcation diagrams illuminating the underlying structure of the models under investigation. These diagrams will identify critical transitions, assess stability, and understand complex behaviours such as oscillations or multistability. By the end of the project, students will have developed a deep understanding of both the mathematical theory and computational methods of bifurcation analysis, as well as practical skills in applying these tools to models in the applied sciences.
Prerequisites
Students should be familiar with basic concepts in differential equations. Coding is a significant aspect of this project, and students should expect to spend time coding and using specialist software packages for continuation. This project best suits students who have taken Numerical Analysis II.
Resources
Strogatz, S. H. (2001). Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering. [introductory text on nonlinear dynamics].
Seydel, R. (2009). Practical bifurcation and stability analysis (Vol. 5). Springer Science & Business Media.
Veltz, R. (2020). BifurcationKit. jl (Doctoral dissertation, Inria Sophia-Antipolis).