The following project proposal is for third-year students taking the mathematical sciences final-year undergraduate project module for the academic year 2024/2025. This project will be jointly supervised with Dr Andrew Krause.
Simple nonlinear systems can display a wide array of interesting dynamics and often help us to understand the mechanisms behind complex real-world phenomena. When nonlinear systems are forced, either by “noise” or a deterministic external signal, new unexpected behavior not predicted by the properties of the original system can arise.
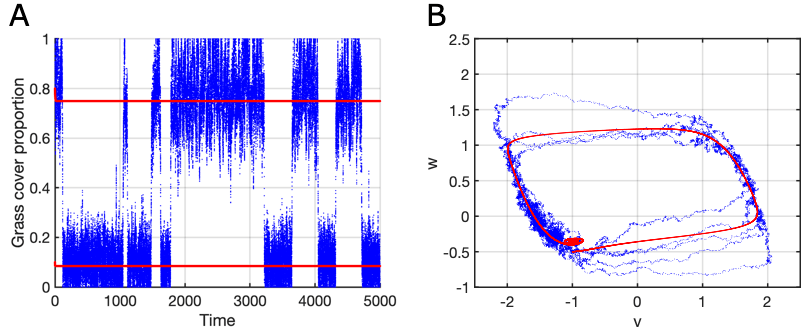
Figure 1A below shows two deterministic trajectories (in red) of a simple ecological model with two alternative stable states, forest and grassland; one trajectory approaches the high-grass state and one approaches the low-grass (forest) state as time advances. However, the single stochastic trajectory in blue switches between the grass and forest states, which is impossible in the deterministic system. This phenomenon is typically called noise-induced switching. Figure 1B shows trajectories of the Fitzhugh-Nagumo model of neuronal dynamics in the phase space. The red deterministic trajectory starts at (-1, -0.5) and eventually settles to a steady state after one sojourn to the right of its starting point. The noisy blue trajectory starts from the same point but never settles to a steady state and exhibits oscillatory behavior for all times; the phenomenon of oscillations created by stochastic forcing is referred to as stochastic resonance.
In this project, students will initially learn how to numerically solve nonlinear ordinary differential equations and simulate solutions to stochastic differential equations. They will then investigate some well-known examples of noise-induced & deterministically forced dynamics in models from ecology, neuroscience, biology and physics. Forcing by a deterministic periodic signal is also widely studied in applications and can lead naturally to projects in non-autonomous dynamics. Depending on individual interests, students could then decide to analyze more complex examples (e.g. spatial or network models), build their own model system for investigation, or delve into more analytic aspects of stochastic dynamics (e.g. Fokker-Planck equations, results in the small noise limit, etc.).
Prerequisites
Students should be familiar with basic concepts in differential equations and probability theory. Prior coding experience and an interest in mathematical modeling in the applied sciences would be useful but no advanced knowledge of dynamical systems or stochastic processes is required. This project would be complementary to and synergize well with Mathematical Biology III and Dynamical Systems III.
Resources
Nonlinear Dynamics and Chaos by Steven Strogatz [introductory text on nonlinear dynamics].
Stochastic Modeling of Reaction-Diffusion Processes by Erban and Chapman [simulation of stochastic processes and examples of noise-induced phenomena]
Lindner, B., Garcıa-Ojalvo, J., Neiman, A. and Schimansky-Geier, L. (2004). Effects of noise in excitable systems. Physics reports, 392(6), pp.321-424. [review of noise-induced phenomena in neuroscience]